My Blogs
A Gentle Introduction to The Game of Life

A Gentle Introduction to The Game of Life

YASH GOSAVI's photo
YASH GOSAVI
·

5 min read

Table of contents

Introduction

John Von Neumann, one of the most influential and famous computer scientists of this era was passionate about space colonization. He thought of sending robots to Mars. As we all know Mars is Red Planet, and it is covered with iron oxides. The robots were supposed to smelt it and collect the iron. The robots would use this smelted iron to make replicas of themselves. Also as a byproduct O2 would be released. This won't be enough for creating an atmosphere but we could create a dome of O2 gas. It was a great plan but there was an issue. How can a robot make a replica of itself? A machine that makes a replica of itself should be quite complicated and the machine to make that machine must be even more complicated resulting in an infinite loop. But it's how we humans work our RNA has all the instructions we need to create a replica of ourselves. Let's say it is tape. Similarly, we can provide a machine with its tape so that it can build a new machine.

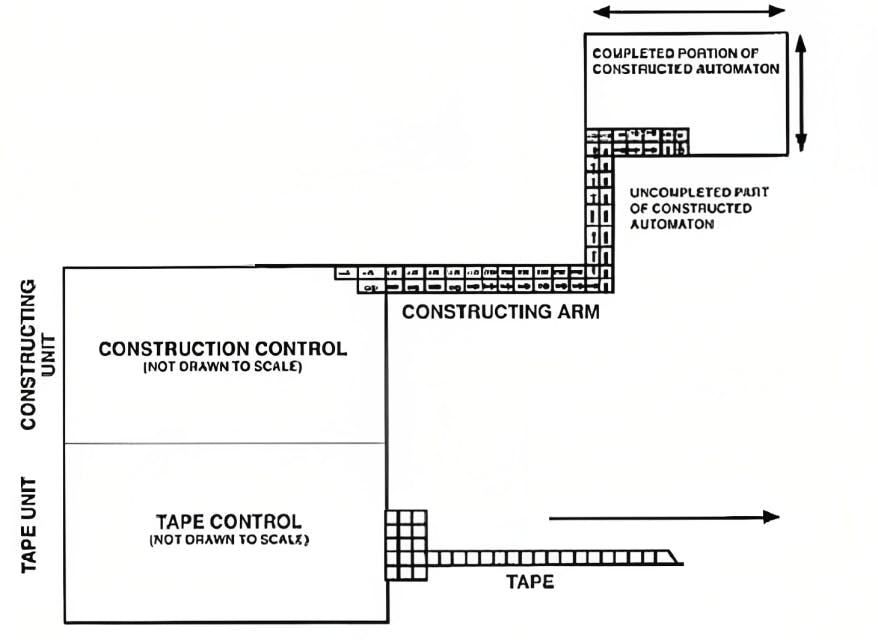
At the same time, Ulam and Neumann created a method to calculate the liquid motion. The key idea was to consider each liquid particle as a discrete unit, and its behavior depended upon its neighbors. This resulted in the ideation of cellular automata. It is in a 2D state, replicating itself algorithmically and had in total of 29 states. So Neumann was able to prove that a particular pattern can make endless copies of itself in a cellular universe

Motivated by these findings and questions in mathematical logic Conway started to work on this problem he considered a variety of 2D cellular automaton rules but with only two states namely alive or dead.

This game behavior was quite fascinating, even though the rules were predefined for different configurations the results were quite different. Algorithmically, there is no way to tell if the configuration will die or it will go on. We have to let the game run for that many generations. Suppose a configuration game doesn't stabilize for 1 million generations, it may stabilize at the 1 billionth generation or will keep on going

Rules of the Game

  1. Any live cell with two or three live neighbors survives.

  2. Any dead cell with three live neighbors becomes a live cell.

  3. All other live cells die in the next generation. Similarly, all other dead cells stay dead.

    With these simple rules and different initial patterns, we can create different "bodies" in the Game of Life. Some may remain still, some may oscillate, some will start moving in a certain direction or some may generate new bodies! For more information, you can read Examples of patterns section from this Wikipedia article

Code:

You can find this code here

We had to create a 2d matrix to hold the state of each cell. So we used NumPy to create a NumPy array. Since I wanted a random configuration we initialized our matrix with

np.random.randint(2, size=dimension)

Since the state of a cell depends on the past state of its neighbors we can't make any changes in the current matrix so we had to create a new matrix. I decided to create a 2D matrix with all cells dead. Now we have to check the state of all the neighbors. The index or surrounding neighbors for a cell at [i, j] will be

1. [i + 1][j + 1]
2. [i][j + 1]
3. [i + 1][j]
4. [i + 1][j - 1]
5. [i - 1][j - 1] 
6. [i][j - 1]
7. [i - 1][j]
8. [i - 1][j - 1]

A point to be noted is, the fate of the cell depends on the sum of states of its neighbors and not their position. So I decided to find their sum. On running the code I realized there was some issue. After some debugging, I realized that count_neighbours was also adding the state of the cell at [i, j]. But then too there is an issue, what about the cells at the edges? I decided to loop them around. So I added the no of rows or columns and took the modulo of it with the no of rows or columns. As you can see below for non-boundary cases the dimension[x] is canceling itself. Also instead of creating a new matrix for every single iteration we copy the new matrix to the old one and the new matrix is then computed. If you are not aware of the modulo operator then click here

old[(i + x + dimension[0]) % dimension[0]][(j + y + dimension[1]) % dimension[1]]

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import animation


dimension = (40, 40)
first = np.random.randint(2, size=dimension)


def animate(frameNum, img, grid):
    next = next_gen(grid)
    img.set_data(next)
    return img


def next_gen(old):
    new = np.zeros(dimension)
    for rows in range(dimension[0]):
        for cols in range(dimension[1]):
            state = old[rows][cols]

            sum = count_neighbours(old, rows, cols)
            if sum == 3 and state == 0:
                state = 1
            elif sum < 2 or sum > 3 and state == 1:
                state = 0

            new[rows][cols] = state
    old[:] = new[:]
    return new


def count_neighbours(old, i, j):
    sum = 0
    for x in range(-1, 2):
        for y in range(-1, 2):
            sum += old[(i + x + dimension[0]) % dimension[0]][
                (j + y + dimension[1]) % dimension[1]
            ]
    sum -= old[i][j]
    return sum


if __name__ == "__main__":
    grid = first
    fig, ax = plt.subplots()
    img = ax.imshow(grid, interpolation="nearest", cmap="gray")
    plt.axis("off")

    update_interval = 50
    anim = animation.FuncAnimation(
        fig, animate, fargs=(img, grid), frames=50, interval=50, save_count=50
    )
    f = r"C:/Users/Yash PC/OneDrive/Desktop/animation.gif"
    writergif = animation.PillowWriter(fps=30)
    anim.save(f, writer=writergif)
    plt.show()

For animating the code I used FuncAnimation class that makes an animation by repeatedly calling a function func. It's present in matplotlib.animation.

Conclusion

Conway's Game of Life is undoubtedly the most successful cellular automaton ever discovered. Unfortunately, Conway passed away during the COVID times, but his work has fascinated many minds for the past 80 years. Since it's Turing Complete one can make actual computers using it. Many have been built on games like Minecraft. Using the "bodies" of the Game of Life many researchers had made Turing machines, a 16-bit computer, and a Game of Life using the Game of Life itself! Hope so you found this blog interesting. Once my institute's final examinations are completed I will try to code it using C like it was done on PDP 8.

algorithmsPython 3